引用
https://www.jianshu.com/p/e136ec79235c
https://zhuanlan.zhihu.com/p/31805309
https://zhuanlan.zhihu.com/p/79980618
https://www.cnblogs.com/zhangbaochong/p/5164994.html
https://blog.csdn.net/qq_25940921/article/details/82183093
这篇文章有毒(错了)
https://www.cnblogs.com/skywang12345/p/3245399.html
二叉查找树(BST)
二叉查找树目的是快速的执行数的,插入,删除,和查询功能。
规则
- 左子树上所有结点的值均小于或等于它的根结点的值。
- 右子树上所有结点的值均大于或等于它的根结点的值。
- 左、右子树也分别为二叉排序树。
- 树中没有键值相等的结点。

实现
- 插入:小的向左,大的向右,直至叶子节点
- 删除:左子树中最大值或右子树中最小值替换待删值,无则为null(左子树的值必然都小于待删值,其中最大值必然是叶子节点或只有左节点的节点,右子树同理)
- 查找:小了向左,大了向右,找到返回,找不到抛错
问题
二叉查找树,其理想的插入,删除,查找的复杂度都在O(logn),但树的不平衡很容易使其退化,直至O(n),其效率不可接受。
平衡二叉树(AVL)
通过旋转,保证树的平衡,达到二叉查找树最优情况
规则
- 任何一个结点的左子树与右子树都是二叉查找树,并且高度之差的绝对值不超过 1。
旋转
- 破坏平衡时的旋转,ps:旋转不会对父节点产生影响
这里的左左,指的是最近失衡点,最先开始的两个方向
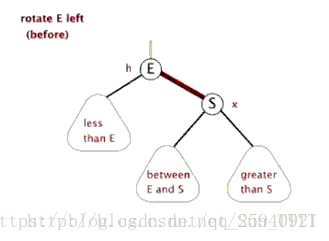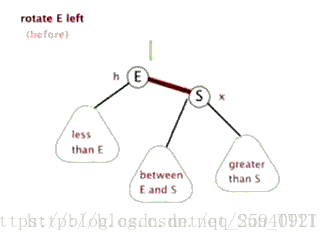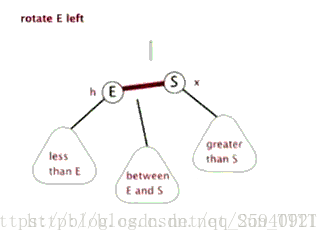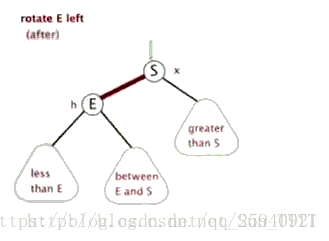
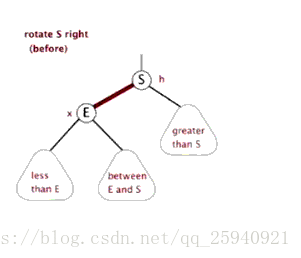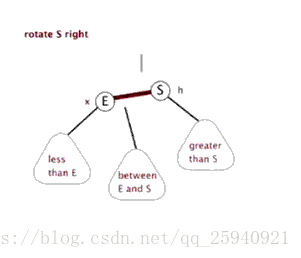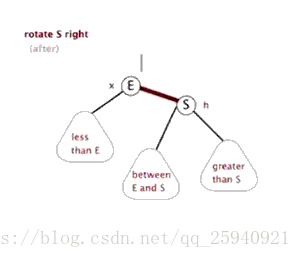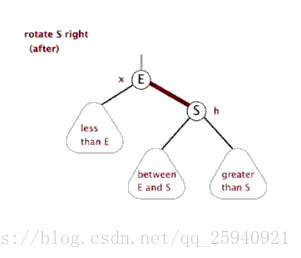
单旋转:左左,右右情况
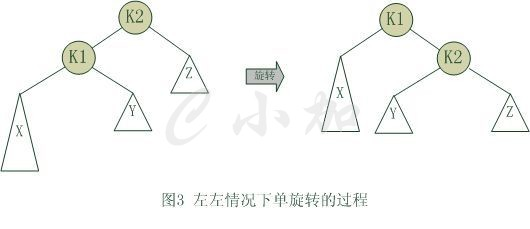
- 从插入点最近的失衡树开始, 如上图K2
- 以失衡点(K2)为基开始反方向旋转(失衡点位于K2左侧,于是右旋)。(K2必然大于K1和Y)
- 附加图
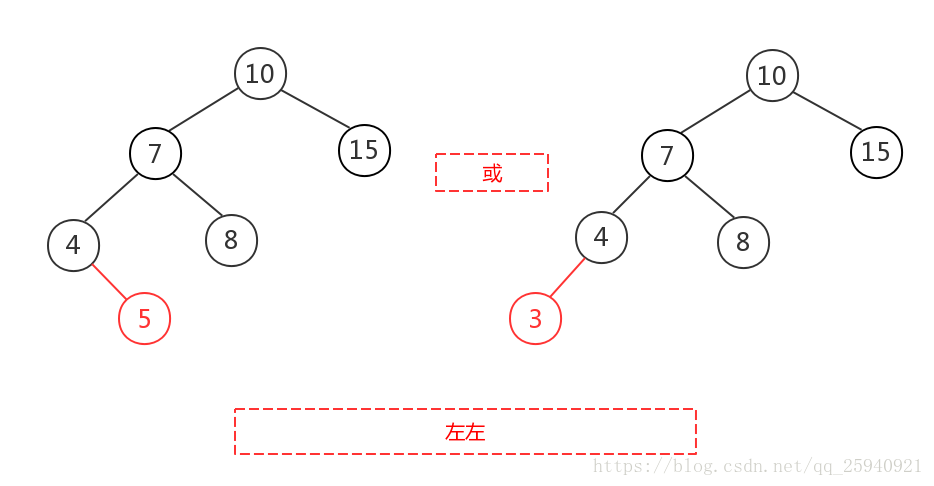

注意与上图的区别
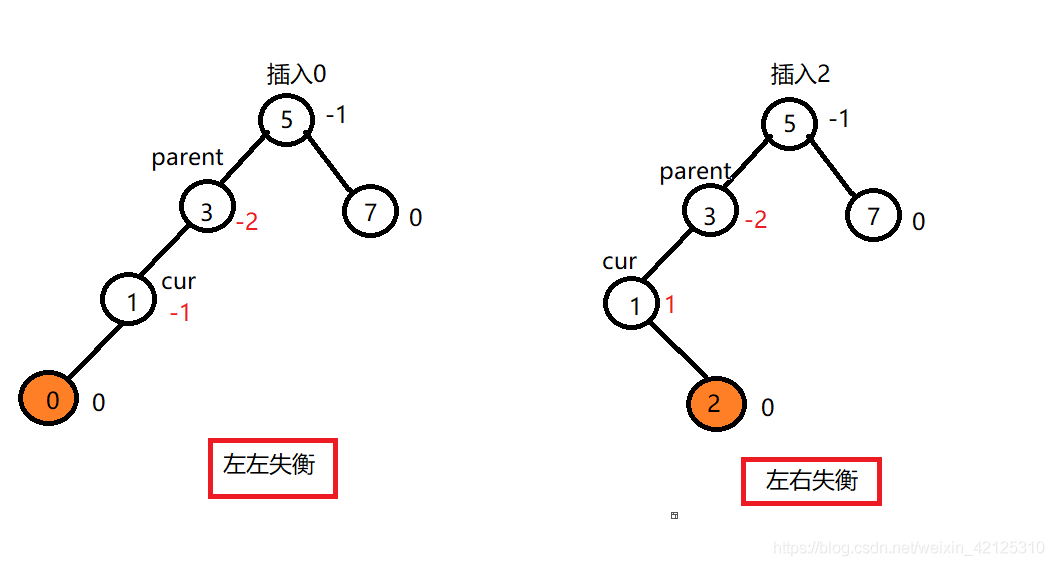
双旋转:左右,右左情况
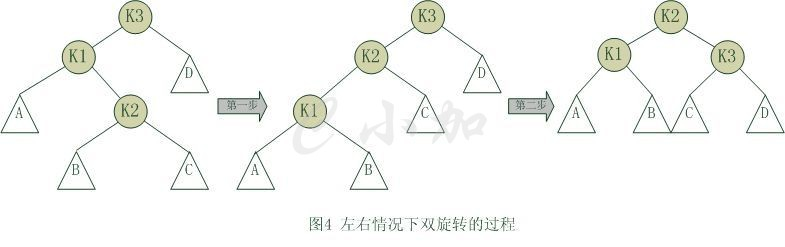
- 从插入点最近的失衡树开始, 如上图K3
- 以失衡点(K3)的**失衡方向点(K1)**为基开使反方向旋转(失衡点位于K1右侧,于是左旋),使之变成先前左左,右右情况
- 以失衡点(K3)为基开始同反方向旋转(失衡点位于K3左侧,于是右旋)
- 附加图
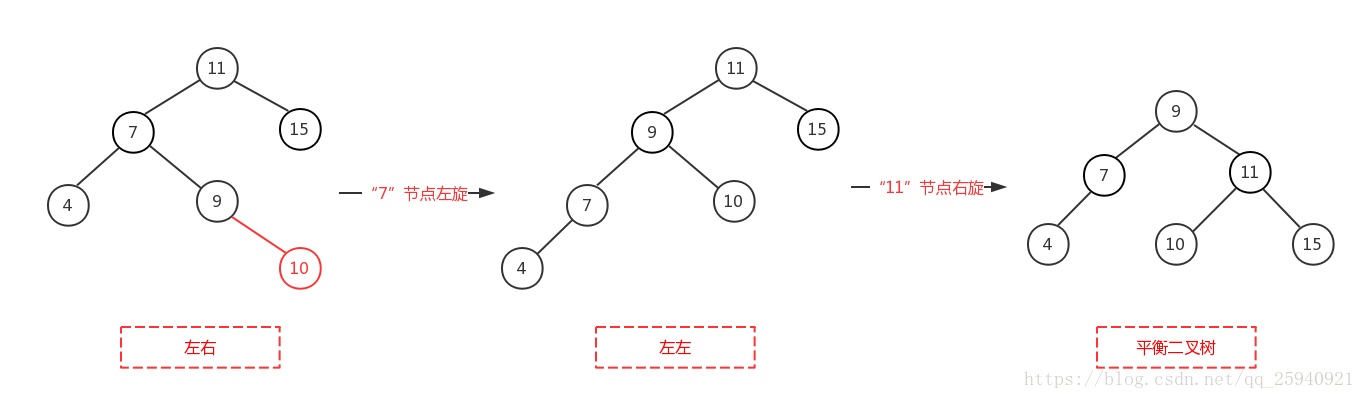
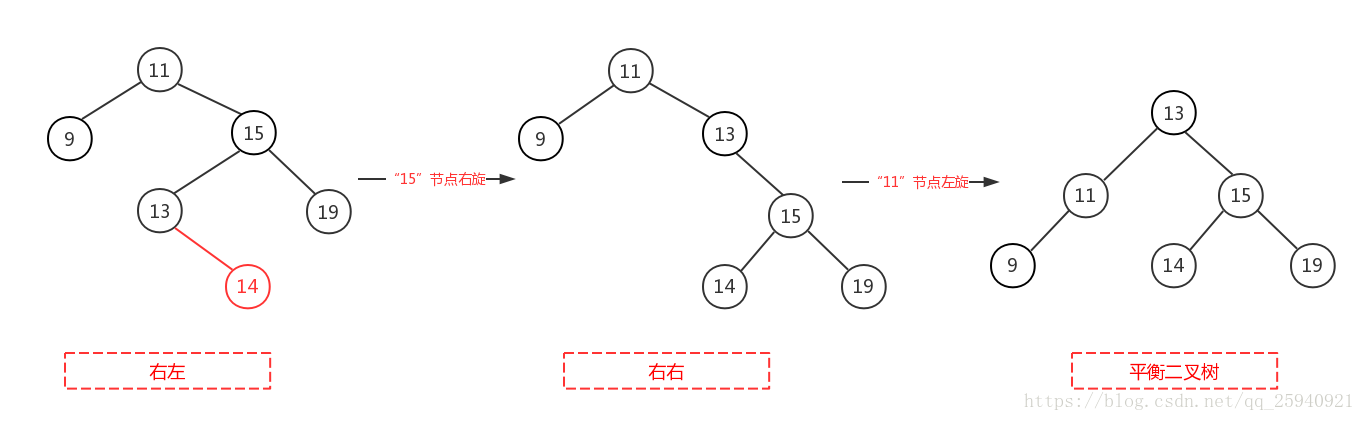
实现
- 插入:与二叉查找树插入方法一致,但当失衡时进行旋转
- 删除:
(1)当删除的节点是叶子节点,则将节点删除,然后从父节点开始,判断是否失衡,如果没有失衡,则再判断父节点的父节点是否失衡,直到根节点,此时到根节点还发现没有失衡,则说此时树是平衡的;如果中间过程发现失衡,则判断属于哪种类型的失衡(左左,左右,右左,右右),然后进行调整。
(2)删除的节点只有左子树或只有右子树,这种情况其实就比删除叶子节点的步骤多一步,就是将节点删除,然后把仅有一支的左子树或右子树替代原有结点的位置,后面的步骤就一样了,从父节点开始,判断是否失衡,如果没有失衡,则再判断父节点的父节点是否失衡,直到根节点,如果中间过程发现失衡,则根据失衡的类型进行调整。
(3)删除的节点既有左子树又有右子树,这种情况又比上面这种多一步,就是中序遍历(结果就是从小到大排列),找到待删除节点的前驱(左边最大)或者后驱(右边最小)都行,然后与待删除节点互换位置,然后把待删除的节点删掉,后面的步骤也是一样,判断是否失衡,然后根据失衡类型进行调整。 - 查找:与二叉查找树插入方法一致
问题
天天旋转,不仅头吃不消,计算机也吃不消啊,虽然复杂度仍都是O(logn),但旋转次数较多。
红黑树
在不过多旋转的情况下,尽可能保证平衡。
规则
1.节点是红色或黑色
2.根节点是黑色
3.每个叶子节点都是黑色的空节点(null)
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点,黑节点可以连续,不仅仅是在叶子上)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
由规则4与规则5可以推出
6. 没有一条路径会比其他路径长出俩倍。所以红黑树是相对平衡
实现
- 插入:与二叉树一样,找到插入位置,尝试插入红节点
(1)当是根节点时直接插入,变成黑节点
(2)当父节点是黑色时直接插入
(3)当父节点是红色时分情况讨论
3.1 叔叔(祖父的另一个节点)结点存在并且为红结点
父节点,叔父节点涂黑,祖父节点涂红
从祖父节点出继续处理
3.2 叔叔结点不存在或为黑结点,父亲结点是左(右)结点,插入节点是左(右)节点
父节点涂黑,祖父节点涂红
对祖父节点进行右旋(左旋)必然不会破坏平衡

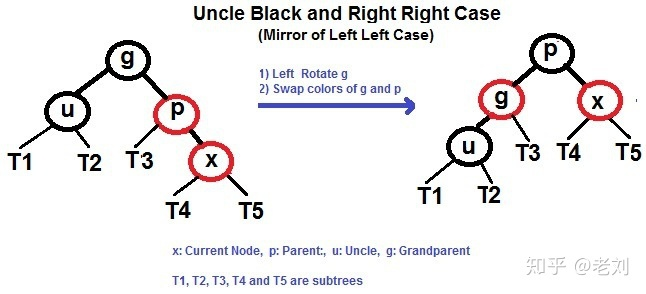
3.3 叔叔结点不存在或为黑结点,父亲结点是左(右)结点,插入节点是右(左)节点
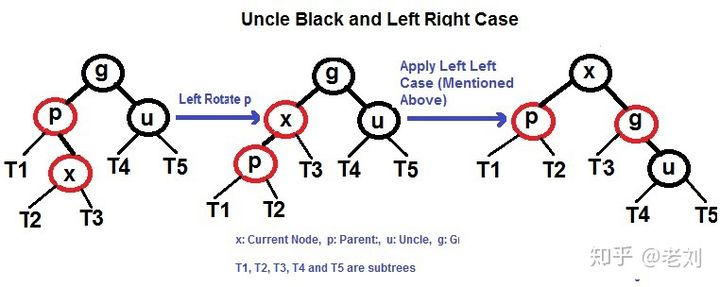
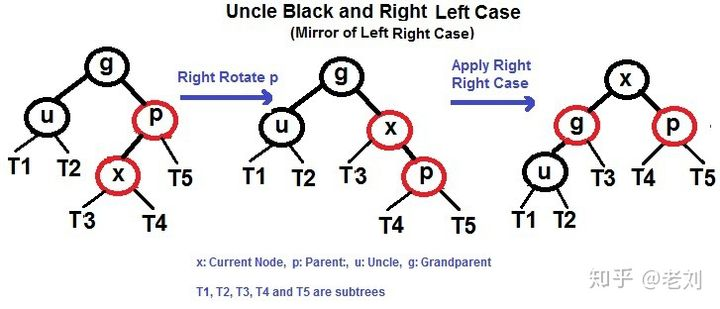
父节点左旋(右旋),形成左左(右右)情况
如3.2处理
- 删除:暂略
- 查找:同查找树一致
问题
红黑树的增,删,查复杂度大概在O(2logn) 相比平衡树的会多一些,但旋转的次数较少,在查询多的情况下可以考虑平衡树。



